Mine and Daniel Stouffer’s paper on how to assess the evolutionary signal of food webs is out on Oikos as an Early View.
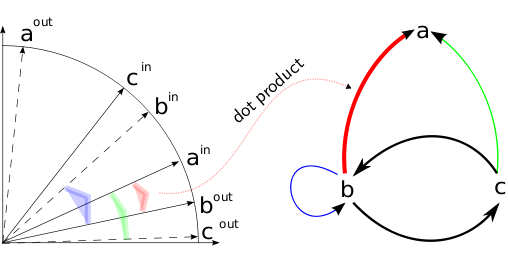
In the paper, we explore some ideas on how to deploy the Random Dot Product Graphs models for food webs. The RDPG framework offers the possibility of moving some questions about the evolution of food webs from a quite rigid, binary framework (that is, the classic interactions matrix representation) to a metric space of species’ abstract functional traits (estimated from that matrix representation). This offers analytical advantages, for example the possibility of speaking about gradual changes in a food web structure.
We are eager to hear your opinion about the proposed approach, and happy to work on future application and developments!
##Abstract
Increasing evidence suggests that an appropriate model for food webs, the network of feeding links in a community of species, should take into account the inherent variability of ecological interactions. Harnessing this variability, we will show that it is useful to interpret empirically observed food webs as realisations of a family of stochastic processes, namely random dot-product graph models. These models provide an ideal extension of food-web models beyond the limitations of current deterministic or partially probabilistic models. As an additional benefit, our RDPG framework enables us to identify the pairwise distance structure given by species’ functional food-web traits: this allows for the natural emergence of ecologically meaningful species groups. Lastly, our results suggest the notion that the evolutionary signature in food webs is already detectable in their stochastic backbones, while the contribution of their fine wiring is arguable.
##Citation
@article{dalla2015exploring,
title={Exploring the evolutionary signature of food webs’ backbones using functional traits},
author={Dalla Riva, Giulio V and Stouffer, Daniel B},
journal={Oikos},
year={2015},
publisher={Wiley Online Library}
}
##Data and Code All the data we used, and the code we wrote, is freely available on a public github repo. let me know if you need more info (I’ll be adding them to the repository shortly).